2. Stabilization
The gain 'stabilization' of gamma spectra is a procedure in which every measured (multichannel) spectrum is shifted in such a way, that the channel axis (the X axis) is converted in an axis displaying gamma energies. The conversion, or 'mapping' function should be such that all peaks present in the spectrum end up at the corresponding gamma energy. For instance, the 40K peak should pop up at 1460 keV, the highest 232Th peak should be found at about 2620 keV.
When importing a new dataset, Gamman will automatically gain stabilize the imported spectra with the standard spectra in the calibration file. This process based on the 'least squares' method computes the lowest possible Chi². From this fit, the concentrations of the nuclides can be derived. However, the problem in 'real life' data is that the positions of the peaks depends on several, detector- and environment-driven factors. Therefore it is advised to always verify the fit of the stabilization.
This chapter will describe how to interpret fit results and verify if the stabilization was correct. And if the fit was incorrect, how to adjust values manually using the stabilization editor.
2.1. Fit results
Every imported data set will automatically be energy stabilized. When the stabilization process is finished, you will see the spectra in the spectral viewer. In this view several parameters are listed in the left menu bar, this topic will discuss these parameters.
Fit results
1. Select a few data points from the data viewer table to get a view similar to the picture below:
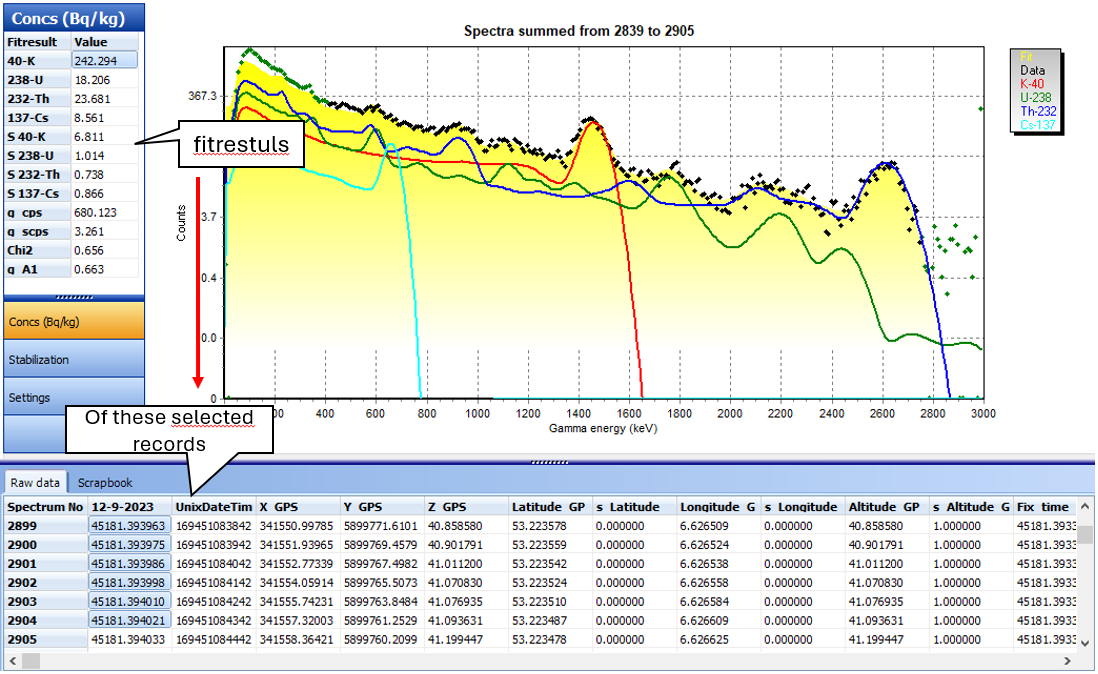
The black dots represent the measured data. Gamman computes which spectrum fits best inside these dots and draws this 'fitted' spectrum (in yellow), the colored lines are the contributing nuclides forming the spectrum. In the left menu bar the result of the fit is shown. The results consist of the nuclide concentrations, the countrate, the standard deviation of the nuclide concentrations and the countrate, the chi2 and the stab factor. The table below contains a description of every item.
1The full spectrum analysis algorithm used by Gamman determines standard errors of estimate. This procedure is based on the standard error of estimate in each channel of the measured spectrum, which equals the square root of the number of counts in the channel. Gamman returns the standard errors of estimate in the same unit as the activity concentrations.
2 The chi2 is a measure for the goodness of the fit. For a statistically perfect fit, the value for chi2 should be close to 1. A larger chi2 means a poor model fit while a chi2 below 1 indicates the model is over-fitting the data. When chi2 equals 1, the statistical variance is in accordance with the statistical error variance. The full spectrum analysis routine used by Gamman assumes no covariance between different spectrum channels. This is correct only when the content of each channel is independent of the content of all other channels. This is not the case whereas photopeaks are distributed over several channels, with the compton edge located in other channels still. Therefore there are fewer degrees of freedom than the model assumes, which leads to an over estimate of the statistical variance. As a result, values of chi2 below 1 can often occur.
For the calculation of chi2, the full spectrum algorithm assumes only a statistical variance between the measured spectrum and the theoretical standard spectra. When there is a non-statistical variance, this will result in an increase of chi2. By increasing the count rate, or by selecting a larger number of spectra, the statistical variance will reduce, while the non-statistical variance remains constant. As a result chi2 squared becomes larger still when more counts are included in the analyzed spectrum
2.2. Stabilization editor and settings
In general, a measured energy spectrum will have a different energy-channel number relationship than the standard spectra used for full spectrum analysis. Various factors (for example crystal temperature, MCA) influence the measurement and can cause 'shifted' energy peaks. In Gamman, the measured spectra will be stabilized using a software algorithm to obtain a spectrum with a fixed energy versus channel number relation. The stabilization editor allows one to change the factors involved in the stabilization algorithm. To obtain best results the fit must be as accurate as possible. Gamman will automatically stabilize your imported data, in some cases this stabilization can be improved using the Stabilization editor.
Changing the stabilization factor
1. The stabilization factor A1 of the records can be changed independently the remaining parameters apply for all records.
2. Click the Stabilization button located in the left menu bar when the program is in spectral view.
3. Adjust the stabilization factors in small steps until the black dots fit the yellow fit as perfect as possible. The step size changing the stabilization can be chosen by placing the cursor insider the box behind one of the digits. By pressing the up and down arrows, this digit will be altered, and the spectrum will be shifted according to the new stabilization factor.
The channels of the standard spectra (i) are related to the channels of the measured spectrum (k) by
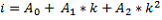
Where A0, A1 and A2 are adjustable coefficients. A0 is an offset which under normal circumstances is a constant and close to zero. A1 is used for linear stabilization and is influenced by the crystal temperature. A2 is used to correct for possible a-linearity of the measurement system and is usually constant and close to zero. For an optimal result of the stabilization algorithm, the lower and upper regions of the energy spectrum may be disregarded. A region can be selected by defining a lower level discriminator (LLD) and an upper level discriminator (ULD). The measured spectrum will be stabilized over the complete energy range, but optimization is done only for the region between the LLD and the ULD. The LLD and the ULD can be set in number of channels of the full scale with respect to the standard spectra.
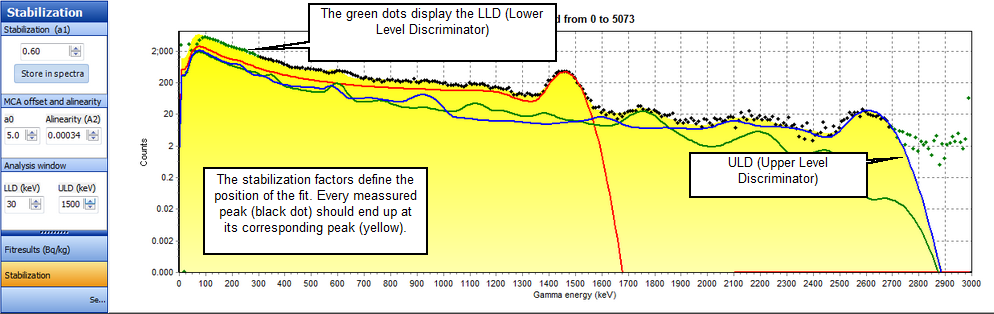
Saving the new stabilization values
The stabilization factor A1 can be stored individually in the selected spectra. If the crystal temperature varied during the survey the fit can be improved by adjusting this value. By pressing the Store in spectra button the values are saved.
2.3. Redo stabilization
The stabilization process is performed when importing a dataset. Sometimes a dataset contains erroneous spectra, for instance caused by electronic drifting or startup problems. This can result in 'strange' looking spectra and an incorrect fit. Such spectra, often characterized by very high or low count rates ('spikes') potentially have a large influence on the quality of the stabilization. If these spikes are detected upon analysis of the dataset they can be removed and the stabilization routine can be re-run using the Redo stabilization option.
Redo stabilization
1. Click Process | Redo stabilization to re-run the stabilization process. This process will also reset all manually configured 'stab' values. Upon choosing to rerun the stabilization algorithm, a dialog will pop-up allowing to set the parameters for stabilization. These settings are quite important for proper stabilization and would normally not be changed by the user. However, it may be needed to adapt the stabilization speed, the LLD or the chi minimum.
the spectrum that will be used in the stabilization update routine. As a rule of thumb, one might remember to use 'fast' stabilization for smaller detector systems (i.e. below 0,5 litre of crystal), and/ or in measurements having low count rates. 'Normal' stabilization can be used for most detector systems and 'normal' count rate measurements (hundred to a few thousand cps). 'Slow' update can be used for large detector systems (> 4L) and high count rate applications.
The second option is the LLD channel to be used in the stabilization routine. This should normally be kept around 50. The 3rd option gives the max chi2 for accepting a stab update. The stabilization algorithm searches a stabilization of the spectrum such that the result of the fit gives a best chi2. The stabilization is said to be proper whenever the chi2 is best, and closest to unity.
More details about the stabilization factors can be found in the Stabilization editor and settings topic.
2.4. Replace MCF data
If your measured spectrum does not fit, it is possible that you accidentally loaded the wrong MCF file with your input data. In such cases you can replace the MCF file that is used to calculate the fit of your input data without creating a new project. Replacing your MCF data will delete possible processed data from your project.
1. Go to Processing | Replace MCF file data.
2. Choose the correct MCF file The Replace MCF algorithm does not redo the stabilization. If after replacing the MCF the fit is still not desirable, then redo the stabilization by choosing Redo Stabilization from the Processing menu.